円柱の表面積は展開図をイメージするところから
うちの子供の場合、円柱の表面積について初めにさらっと教えても、いまいちピンとこないようでした。
どうやら表面積を計算する際にイメージする円柱の展開図について、組み立てると円柱になるということが、いまいちピンときていないようでした。
こんなときは100の言葉で説明するよりも、実際に1度組み立ててみせるに限ります。
切り貼りできるような円柱の展開図を作りましたので、同じところでつまづいているお子さんがいらっしゃるようでしたら、どうぞプリントアウトしてお使いください。
展開図からの表面積の導き方は後半でご説明しています。
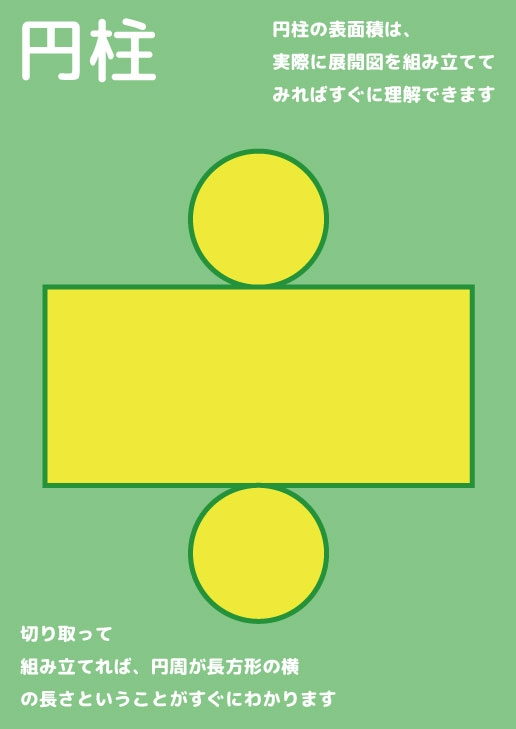
展開図
まずは、頭の中で、展開図は立体図へ、そして立体図であれば展開図へと、コンバート(変換)ができるようになれば、円柱の表面積はもうほとんど理解できたも同然です。
先取り学習でここまで進んできた小さいお子さんでも、これらの図のコンバートが頭の中でカチッとできれば、計算方法もすぐに理解することができるでしょう。
円柱の表面積を求める問題は数学検定5級の頻出問題です。
展開図を切り取り、組み立てながら説明してあげてください。
円柱の表面積のおさらい
理屈がわかっていれば、必ずしも文字式で覚えなくても大丈夫です。
計算方法を説明していきます。
円柱の表面積は、底面と天面の二つの円の面積と長方形の面積を足すことで求めることができます。
そして、それぞれの面積はこのような文字式で表すことができます。
登場する文字の r は半径、πは円周率です。
天面の円 = \(πr^2\)
底面の円 = \(πr^2\)
長方形 = \(2πrh\)
円の面積の文字式 \(πr^2\)は、お子さんも覚えていることでしょう。
念のためにご説明すると、天面と底面の2つの \(πr^2\) なので、天面と底面の面積は、合わせて \(2πr^2\) となります。
では長方形の面積の表し方はどうでしょうか。
長方形はその面積の計算方法の理屈を説明してあげたほうが理解が早いです。
まず大前提として、長方形の面積は、縦×横、もしくは横×縦で計算できます。
ここでは横×縦として考えてみましょう。
展開図を組み立ててみるとよく分かりますが、
円柱の周りの長方形は天面と底面の円の円周をぐるっと回っています。つまり、長方形の横の長さは円周と同じ、ということになります。
円周の公式は、直径×3.14です。そしてそれを文字式にすると\(2πr\)で、長方形の横の長さは、\(2πr\)となります。
次に長方形の縦の長さですが、これは円柱の高さがそれにあたります。
文字式では高さは h とします。
これにより、円柱を展開した際の長方形の面積は、\(2πr\)(横)× \(h\)(高さ)と表せます。
上記の説明全てを合わせますと、円柱の表面積は最初にも紹介したこの公式となります。
長々と説明しましたが、ようは全ての面積を足すということです。
忘れてしまいがちなのは、長方形の横の長さが円周ということくらいでしょう。
先取り学習している小さいお子さんでは、長方形の横の長さ=円周であることを口で説明しても、なかなか伝わらないかもしれません。
でも、展開図を組み立てながら説明すれば、きっとすぐに理解できることでしょう。
ぜひダウンロードして切りとって説明してあげてください。
